強化学習実装入門 (DQN 編)

こんにちは。皆さんは "強化学習" と聞いて、何を想像しますか？

プロ棋士よりも強い囲碁 AI や、ビデオゲームで人間に勝る AI、ルービックキューブを解くことができるロボットアームなど、強化学習にまつわる象徴的な研究結果が数多く出されており、強化学習のポテンシャルに魅力を感じている方も多いのではないでしょうか？

そこで、今日は "実装" をテーマに、強化学習アルゴリズム Deep Q-Network (DQN) を実装しながら、強化学習実装の Tips を共有していきたいと思います。

この記事では、"深層学習の実装経験があり、これから強化学習も触ってみたい方" を対象とします。強化学習の知識は問いませんが、"実装" をテーマにした記事のため、必要な知識は "何となく理解する" ことにフォーカスして解説します。実際に PyTorch を用いて DQN を実装していくことで、強化学習の実装の大まかな流れを理解し、今後それをベースに色々なアルゴリズムを実装できるようになることを、この記事のゴールとします。

また、計算資源を持っていない方でも簡単に実装・検証いただけるよう、Atari のビデオゲームを簡略化した環境 MinAtar のブロック崩し (Breakout) を利用します。この記事を読み進めることで、実際に以下のような AI を作成していきます！

それでは、早速 DQN 実装のハンズオンを始めましょう。

アルゴリズムのおさらい

実装の前に、DQN のアルゴリズムの概要をおさらいしておきましょう。ここでは、DQN のアルゴリズムを "何となく" 理解することを目的とします。より厳密な議論は、他の文献を参照ください。

強化学習とは

強化学習では、"エージェント" がある "環境" において、行動して報酬を受け取り、また行動して報酬を受け取り、$\cdots$ を繰り返しながら、受け取る報酬の総和を最大化することを目的とします。

もう少し具体化すると、時刻 $t \;(\ge 0)$ において、環境の状態が $s_t$ のときに、エージェントが行動 $a_t$ を行ったとします。このとき、環境は一定のルール (次式) にしたがって、次の状態 $s_{t+1}$ と報酬 $r_t$ を計算し、エージェントに返します。(報酬 $r_t$ も確率分布に従うように定式化することもあります。)

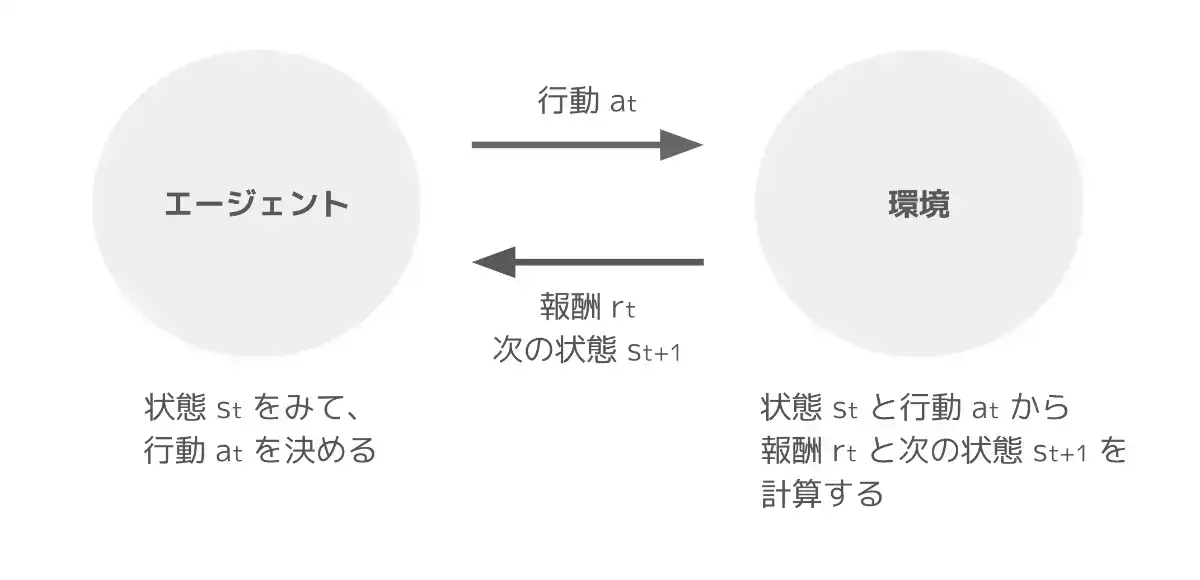
この "行動して、報酬と次の状態を受け取る" という一連の流れを繰り返しながら、累積報酬 $\sum_{t=0} r_t$ を最大化するような行動指針を求めることが、強化学習の目的となります。このとき、この行動指針のことを "方策" と呼びます。

今回利用する環境では、状態は "ブロック崩しのゲーム画面"、行動は "右 / 左 / 何もしない" のいずれかで、ブロックを 1 つ崩すたびに +1 の報酬が与えられます。このとき、ゲーム開始 ($t=0$) からゲームオーバーまでの一連の流れを "エピソード" と呼びます。

エージェントが、試行錯誤を繰り返しながら報酬をより多くもらえるように方策を修正していくのが、強化学習の大まかな流れです。

Q 学習とは

多くの強化学習アルゴリズムでは、累積報酬ではなく、割引率 $\gamma \in [0, 1)$ を用いた割引累積報酬 $\sum_{t=0} \gamma^t r_t \;\; (= r_0 + \gamma r_1 + \gamma^2 r_2 + \cdots)$ を最大化します。つまり、将来貰える報酬は、今すぐに貰える報酬よりも価値が低くなるように割引いて計算します。累積報酬は発散してしまう可能性があるため、割引累積報酬を使うことで、アルゴリズムの収束性の議論が容易になるメリットがあります。

では、まず方策 $\pi$ に関する状態価値関数 $V^\pi (s)$ と行動価値関数 $Q^\pi (s, a)$ を定義します。状態価値関数 $V^\pi (s)$ は、"状態 $s$ からスタートして、方策 $\pi$ に従い続けたときの割引累積報酬の期待値" です。(期待値は、環境の状態遷移 $P$ と方策 $\pi$ に関して計算します。)

また、行動価値関数 $Q^\pi (s, a)$ は、"状態 $s$ で行動 $a$ を行った瞬間からスタートして、方策 $\pi$ に従い続けたときの割引累積報酬の期待値" です。

つまり、これらの価値関数は、"この状態にいるってことは、今後このくらいの (割引) 報酬が貰えそうだな"、"この状態でこの行動を取ったら、今後このくらいの (割引) 報酬が貰えそうだな" といった、状態 (もしくは状態と行動) の価値を表していると解釈できます。

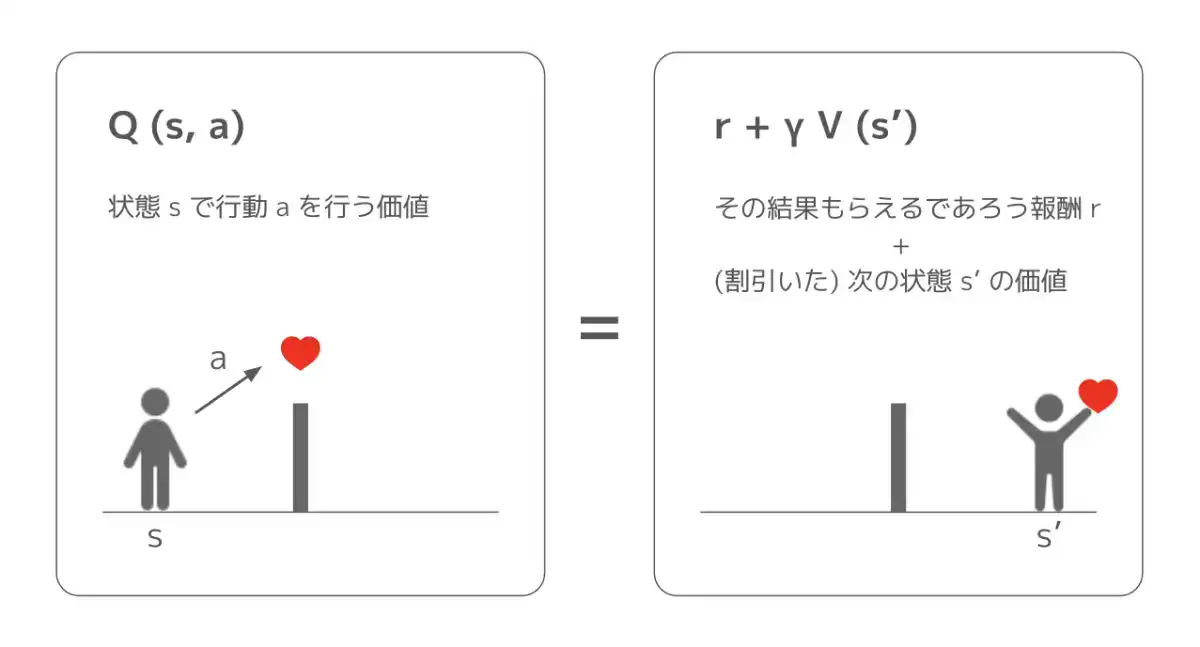
証明は省きますが、これらの価値関数の間には、以下のような関係が成り立ちます。

これは、(期待値の意味で) "ある状態である行動を取ることの価値" は "その結果貰える報酬と次の状態の価値の和" と等しいと解釈できますね。ただし、次の状態の価値は 1 時刻先の価値なので、割引しています。

ここで、強化学習が最終的に発見したい、最適な方策 $\pi^*$ を考えてみましょう。最適な方策の行動価値関数 $Q^{\pi^*}$ が分かれば、あとはどんな状態 $s$ においても、行動価値を最大化する行動 $a^* = \mathop{\rm argmax}\limits_{a} Q^{\pi^*}(s, a)$ を選択することで、割引累積報酬の期待値を最大化できます。

したがって、最適な方策の行動価値関数を単に "最適行動価値関数" と呼ぶと、最適行動価値関数が分かれば、最適な方策も計算でき、解きたいタスク (今回はブロック崩し) において最強の AI を作れるんですね！

最適な方策では、常に行動価値を最大化する行動を取るので $V^{\pi^*}(s) = \max\limits_{a} Q^{\pi^*}(s, a)$ が成り立ちます。したがって、最適行動価値関数を $Q^*(s, a)$ と表すと、以下の関係性が成り立ちます。

Q 学習では、式 (1) を満たす方向に行動価値関数の推定値を更新していくことで、最適行動価値関数を求めていきます。具体的には、学習率を $\alpha$ とすると、以下の更新式を繰り返し適用し、推定値を更新します。

上式では、現時刻の行動価値の推定値 $\hat Q(s_t, a_t)$ を、次時刻の行動価値の推定値から計算される目標値 $r_t + \gamma \max\limits_{a} \hat Q(s_{t+1}, a)$ に近づけていると解釈できます。この Q 学習は、ある一定の条件下で最適行動価値関数に収束することが知られています。

DQN とは

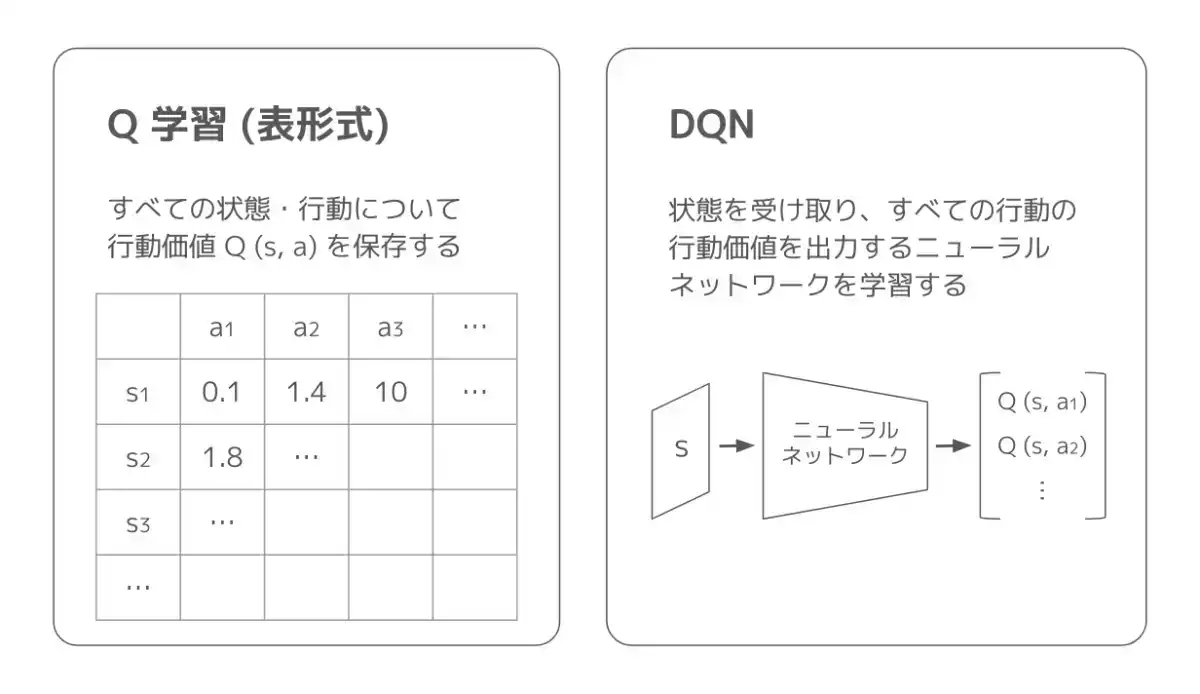
Q 学習では、一般的にすべての状態と行動に関して、行動価値を表形式で保存しておき、少しずつその表を更新していきます。そのため、状態の次元数が増えていったり、画像などの "連続値" を状態とする場合、計算量が膨大になってしまうという課題があります。

そこで DQN では、行動価値関数 $Q^\pi(s, a)$ を、"状態を受け取り、すべての行動について行動価値を出力するニューラルネットワーク" で近似します。そうすることで、状態が高次元・連続値の場合でも学習可能となります。

DQN では、以下の損失関数でネットワークの最適化を行います。(元論文では Huber Loss を用いていますが、今回は学習を速めるために L2 Loss を使います。)

この損失関数では、Q 学習と同様に "現時刻の行動価値の推定値を、次時刻の行動価値の推定値から計算される目標値に近づける" ようにパラメータを更新していると解釈できます。これにより、式 (1) を満たす (最適行動価値関数に近づく) 方向に、行動価値関数の推定値 $Q_\theta$ を更新しているのですね。

ただし、"現時刻の推定値" と "目標値" を同時に動かしてしまうと学習が不安定になってしまうため、目標値 $r_t + \gamma \max\limits_a Q_{\bar \theta}(s_{t+1}, a)$ は、別のパラメータ $\bar \theta$ を用いて計算します。具体的には、$\theta$ の更新を N 回行う度に $\bar \theta \leftarrow \theta$ とし、その N 回の間、$\bar \theta$ は固定しておきます。こうすることで、目標値が時々刻々と変化して、学習が不安定になるのを防ぐことができます。このような、安定して目標値を計算するためのネットワーク $Q_{\bar \theta}$ を "ターゲットネットワーク" と呼びます。

また、あえて最適な行動ではなくランダムに行動し、より多様なデータを集めることで、強化学習の効率を向上させるテクニックが存在します。これを "探索" と呼びます。DQN では、一定の確率 $\epsilon$ でランダムに行動することで、探索を行います。

以下に、DQN アルゴリズムを使った際の大まかな学習の流れを示します。

• パラメータ $\theta$ を初期化し、$\bar \theta \leftarrow \theta$ とする
• 環境を初期化し、状態 $s$ を受け取る
• 以下を繰り返す
  • 行動 $a$ を計算する
    • 確率 $\epsilon$ でランダムな行動
    • そうでなければ、現時点で最適な行動 $\mathop{\rm argmax}\limits_{a'} Q_\theta(s, a')$
  • 行動 $a$ を行い、次の状態 $s'$ と報酬 $r$ を受け取る
  • データ $(s, a, r, s')$ を保存する
  • 過去のデータを用いて、式 (2) の損失関数をもとに $\theta$ を更新する
  • N 回に 1 回、$\bar \theta \leftarrow \theta$ とする

DQN 実装ハンズオン

それでは、本題の "実装" に入っていきましょう！全体のコードは GitHub 上で公開しています。以下のボタンをクリックすると、Amazon SageMaker Studio Lab (使い方) または Google Colaboratory 上でコードを開けます。

今回の DQN 実装で出てくる主なコンポーネントは、以下の 5 つです。

• 環境 (PyTorchEnv) : OpenAI Gym 互換のインターフェースを持った環境。今回は、MinAtar の環境を、PyTorch で扱いやすいようにラップします。
• リプレイバッファ (ReplayBuffer) : 収集したデータを保存するためのストレージ。
• ネットワーク (QNetwork) : 行動価値関数を近似するニューラルネットワーク。
• アルゴリズム (DQN) : アルゴリズムのコア部分。今後、類似のアルゴリズムを実装することを考えて、アルゴリズム共通のインターフェースを持つように実装します。
• メインプロセス : 上記 4 つのコンポーネントを利用しながら、実際に学習を行う部分。実験管理やハイパラチューニングなど、より汎用的に利用したい場合には、Trainer クラスを作成することを検討してください。

また、この記事では、以下のライブラリを利用します。(後ほどの可視化のために、MinAtar のソースコードを少し修正しています。)

git+https://github.com/toshikwa/MinAtar.git@faf6d1fde3429c9e810ae2d2bfd377f7abeafb34
gym==0.23.1
numpy==1.21.5
torch==1.11.0
tensorboard==2.8.0

import os
from datetime import datetime
from collections import deque

import gym
import numpy as np
import torch
from torch.utils.tensorboard import SummaryWriter

gym.logger.set_level(40)

環境 (PyTorchEnv)

まず、強化学習を行う環境を実装していきます。OpenAI Gym 互換のインターフェースを持つように実装するのが一般的なので、プログラムの再利用性を高めるためにも、これに従うのが良いでしょう。インターフェースの詳細はドキュメントに書いてありますが、gym.Env を継承したクラスを作成し、以下の 4 つのメソッドを実装する必要があります。

• step(self, action) : 現在の状態と受け取った行動から、"(次の状態, 報酬, 終了信号, 補足情報)" を計算し、返します。今回、行動 action は "行動の選択肢に 0 から順に振った int 型の数字" で表されます。また "終了信号" は、そのエピソードが終了したかどうかの真偽値です。
• reset(self) : 環境を初期化し、エピソードの初期状態を返します。通常、環境作成時と、step から返される終了信号が true の場合に呼び出します。
• render(self, mode="human") : ゲーム画面など、環境の状態を描画します。mode には、GUI 上に描画を行う human や、画像の RGB 行列を返す rgb_array などが指定されます。
• close(self) : 環境を終了し、インスタンスを破棄します。

MinAtar では、すでに Gym 互換の環境を作成してくれてるので、実装する必要はありません(が、このインターフェースはよく利用するのでここで覚えてしまいましょう)。ただ、利用する環境では、状態は "(縦, 横, チャンネル)" の次元を持つ画像として返されるので、PyTorch で扱うために "(チャンネル, 縦, 横)" と返すようにラップしてあげましょう。

Gym では、環境の状態を修正するためのラッパー ObservationWrapper を用意してくれているので、これを利用します。

class PyTorchEnv(gym.ObservationWrapper):
    def __init__(self, env):
        super(PyTorchEnv, self).__init__(env)

        # 状態空間の定義。元の環境の (縦, 横, チャンネル) から
        # (チャンネル, 縦, 横) に変更する。
        # (Box では、[low, high] の連続値で構成される dtype 型の
        # shape 次元配列を、状態として定義できる。)
        self.observation_space = gym.spaces.Box(
            low=0.0,
            high=1.0,
            shape=(
                env.observation_space.shape[2],
                env.observation_space.shape[0],
                env.observation_space.shape[1],
            ),
            dtype=np.float32,
        )

    def observation(self, observation):
        # ここで、実際に状態を修正する。
        # 引数には、元の環境の状態が渡される。
        return np.transpose(observation, (2, 0, 1))

MinAtar の環境をこのクラスでラップすることで、PyTorch で扱いやすい形で環境を作成できます。

リプレイバッファ (ReplayBuffer)

続いて、式 (2) の損失関数を計算するのに必要なデータを保存するためのストレージを実装します。強化学習では、このストレージを "リプレイバッファ" と呼んだりします。

式 (2) の損失関数を計算するには、状態 $s_t$, 行動 $a_t$, 報酬 $r_t$, 終了信号 $d_t$, 次の状態 $s_{t+1}$ が必要です。ここで、終了信号は、"エピソードが終了したかどうか" を表す真偽値です。では、なぜ終了信号が必要なのでしょうか？

時刻 $t$ において、状態 $s_t$ で行動 $a_t$ を行った結果、エピソードが終了した場合、どのような方策であっても行動価値関数は $Q(s_t, a_t) = r_t$ となります。(行動価値関数の定義は、 "状態 $s$ で行動 $a$ を行った瞬間からスタートして、方策 $\pi$ に従い続けたときの割引累積報酬の期待値" でしたね？) すなわち、時刻 $t$ でエピソードが終了した場合、$Q_\theta(s_t, a_t)$ が $r_t$ に近づくように学習する必要があります。

このとき、終了信号 $d_t$ を保存しておいて、以下の損失関数を用いるように修正することで、エピソードが終了したかに関わらず、同じ損失関数を用いることが可能になります。

では、append メソッドで "(状態, 行動, 報酬, 終了信号, 次の状態)" を保存し、sample メソッドでバッチサイズ分をサンプルする ReplayBuffer クラスを実装しましょう。

class ReplayBuffer:
    def __init__(
        self,
        buffer_size,
        state_space,
        device,
    ):
        # (状態, 行動, 報酬, 終了信号, 次の状態) の torch.tensor を初期化する。
        self.state = torch.empty((buffer_size, *state_space.shape), dtype=torch.float32, device=device)
        self.action = torch.empty((buffer_size, 1), dtype=torch.int64, device=device)
        self.reward = torch.empty((buffer_size, 1), dtype=torch.float32, device=device)
        self.done = torch.empty((buffer_size, 1), dtype=torch.float32, device=device)
        self.next_state = torch.empty((buffer_size, *state_space.shape), dtype=torch.float32, device=device)

        # 最大データ数
        self.buffer_size = buffer_size
        # データ数
        self._n = 0
        # 次にデータを挿入する位置
        self._p = 0

    def append(self, state, action, reward, done, next_state):
        # データを挿入する。
        self.state[self._p] = torch.tensor(state, dtype=torch.float32)
        self.action[self._p] = action
        self.reward[self._p] = float(reward)
        self.done[self._p] = float(done)
        self.next_state[self._p] = torch.tensor(next_state, dtype=torch.float32)

        # (最大データ数を超えないように) データ数を更新する。
        self._n = min(self._n + 1, self.buffer_size)
        # 次にデータを挿入する位置を更新する。
        # (データが一杯になったら、一番古いデータから順に上書きする。)
        self._p = (self._p + 1) % self.buffer_size

    def sample(self, batch_size):
        # バッチサイズ分のデータのインデックスを、ランダムにサンプルする。
        idxes = np.random.randint(low=0, high=self._n, size=batch_size)
        # (状態, 行動, 報酬, 終了信号, 次の状態) を返す。
        return (
            self.state[idxes],
            self.action[idxes],
            self.reward[idxes],
            self.done[idxes],
            self.next_state[idxes],
        )

シンプルな実装ですが、以下の 2 点に注意しています。

• torch.tensor を使わなくても、Python のリストに追加していく形で実装することも可能です。が、"明示的に型と次元を指定することで可読性が向上する"、"ストレージを GPU 上に確保できる" というメリットがあります。ただし、画像を扱う際には、GPU メモリに収まるか注意しましょう。
• 実は、今回は "次の状態" を保存しなくても、"状態" だけ保存して state[i] と state[i+1] を利用することも可能です。が、明示的に "次の状態" を保存しておくと、今後リプレイバッファを拡張しやすくなります。

ネットワーク (QNetwork)

続いて、行動価値関数を近似するニューラルネットワーク $Q_\theta(s, a)$ を表す QNetwork を実装します。 ここで、"状態を入力として受け取り、全ての行動について行動価値を出力する" ようなネットワークを構築することで、損失関数内の $\max\limits_a Q$ も 1 回の順伝搬で計算できるようになります。

今回用いる環境の状態は、4 x 10 x 10 の画像のテンソルなので、その次元のテンソルを受け取り、行動の数 (num_actions) だけスカラー (行動価値) を出力するように実装しましょう。

class QNetwork(torch.nn.Module):
    def __init__(self, num_actions: int):
        super(QNetwork, self).__init__()

        # Convolutional レイヤ
        self.conv_net = torch.nn.Sequential(
            torch.nn.Conv2d(4, 16, kernel_size=3, stride=1),
            torch.nn.ReLU(),
        )

        # Fully-connected レイヤ
        self.fc_net = torch.nn.Sequential(
            torch.nn.Linear(in_features=8 * 8 * 16, out_features=128),
            torch.nn.ReLU(),
            torch.nn.Linear(in_features=128, out_features=num_actions),
        )

    def forward(self, x):
        x = self.conv_net(x)  # (B, 4, 10, 10) => (B, 16, 8, 8)
        x = x.view(x.size(0), -1)  # (B, 16, 8, 8, 16) => (B, 16 * 8 * 8)
        x = self.fc_net(x)  # (B, 16 * 8 * 8) => (B, num_actions)
        return x

    def select_action(self, state: torch.tensor) -> int:
        # この部分の計算は損失関数に出てこず、勾配を計算しなくてよいので、勾配計算を無効化する。
        with torch.no_grad():
            # 状態 (torch.tensor) を受け取り、行動価値が最大となる行動を計算する。
            # (state は状態 1 つ分なので、バッチの次元を追加してから計算する。)
            action = self.forward(state.unsqueeze(0)).argmax().item()
        return action

ここで、select_action メソッドも実装しています。このメソッドでは、状態 state を 1 つ受け取り、"行動価値が最大になる行動" を出力します。言い換えると、"現在の行動価値関数の推定値に基づいた最適な行動" を選択するメソッドです。

アルゴリズム (DQN)

それでは、アルゴリズムのコア部分を実装していきましょう。ここで実装する DQN クラスは、類似アルゴリズムを実装する際にも共通インターフェースを持つように、以下のメソッドを実装します。ここで、step は、学習におけるトータルの環境の状態遷移回数を表します。

• is_random(self, step) : step 回目の反復時に、"探索するか" を計算します。
• is_update(self, step) : step 回目の反復時に、"ネットワークのパラメータを更新するか" を計算します。例えば、"一定量のデータが貯まるまでは学習を行わない" ことがあります。
• is_update_target(self, step) : step 回目の反復時に、"ターゲットネットワークのパラメータを更新するか" を計算します。ここでは N 回に 1 回更新を行います。
• update(self, batch) : 実際に、ネットワークを 1 回更新する関数です。
• update_target(self) : 実際に、ターゲットネットワークを 1 回更新する関数です。

コンストラクタ

まず、DQN クラスのコンストラクタです。強化学習では、データが少ない状態で最適化を始めてしまうと、少ないデータに過適合してしまい、学習がうまく進まなくなることがあります。そこで、start_steps 分のデータが集まってから学習を開始するように実装していきます。

class DQN:
    def __init__(
        self,
        q_net: QNetwork,
        target_net: QNetwork,
        lr: float,
        gamma: float,
        start_steps: int,
        epsilon: float,
        update_interval: int,
        target_update_interval: int,
    ):
        # ネットワーク
        self.q_net = q_net
        # ターゲットネットワーク
        self.target_net = target_net
        # ターゲットネットワークのパラメータを、ネットワークのパラメータと同期する。
        self.update_target()

        # ニューラルネットワークの最適化を行う Optimizer
        self.optimizer = torch.optim.RMSprop(self.q_net.parameters(), lr=lr)

        # 割引率
        self.gamma = gamma
        # 学習を始めるのに必要なデータの数
        self.start_steps = start_steps
        # 探索を行う確率
        self.epsilon = epsilon
        # ネットワークを更新する頻度 (今回は、行動するたびネットワークを更新するので 1 とする。)
        self.update_interval = update_interval
        # ターゲットネットワークを更新する頻度
        self.target_update_interval = target_update_interval

is_random(self, step)

start_steps 分のデータが集まるまでは、ランダムに行動します。それ以降は、確率 $\epsilon$ でランダムに行動します。

    def is_random(self, step):
        return step < self.start_steps or np.random.rand() < self.epsilon

is_update(self, step)

start_steps 分のデータが集まるまでは、ネットワークは更新しません。それ以降は、一定のインターバルで (今回は行動するたびに) ネットワークを更新します。

    def is_update(self, step):
        return step >= self.start_steps and step % self.update_interval == 0

is_update_target(self, step)

start_steps 分のデータが集まるまでは、ターゲットネットワークは更新しません。それ以降は、一定のインターバルでターゲットネットワークを更新します。

    def is_update_target(self, step):
        return step >= self.start_steps and step % self.target_update_interval == 0

update(self, batch)

では、パラメータ更新を行うメソッドを実装していきましょう。ここでは、再利用性のために "損失関数を計算するメソッド" も分けて実装します。この関数の引数は、それぞれバッチサイズ分の状態、行動、報酬、終了信号、次の状態です。

まず、ネットワークは状態 state を受け取り、全ての行動について行動価値 output を出力します。ここから、実際に行った行動 action の行動価値を取り出すことで、現時刻の行動価値の推定値 curr_q を計算します。

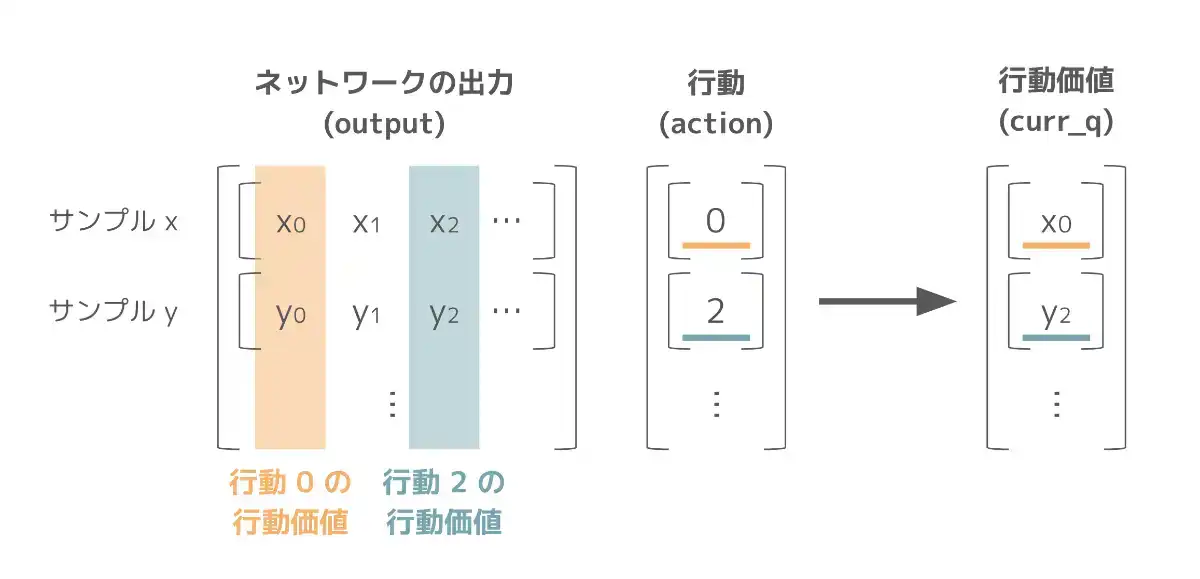
これは、torch.gather を利用することで curr_q = output.gather(dim=1, index=action) と計算できます。

続いて、次の状態 next_state をターゲットネットワークに渡すことで、次時刻の全ての行動の行動価値を計算します。これに torch.max を適用して、$\max\limits_a Q_{\bar \theta}(s_{t+1}, a)$ を計算します。torch.max は、最大値だけではなく、そのインデックスも返却する点に注意します。

現在の行動価値の推定値と、目標値を計算したら、あとは L2 loss を計算するだけです。

    def calculate_loss(self, state, action, reward, done, next_state):
        # 現在の行動価値の推定値を計算する。
        output = self.q_net(state)
        curr_q = output.gather(1, action)

        # 目標値を計算する。
        with torch.no_grad():
            next_v = torch.max(self.target_net(next_state), dim=1, keepdim=True).values
            # (エピソードが終了した場合、(1 - done) は 0 となり、目標値は r_t となります。)
            target_q = reward + self.gamma * (1 - done) * next_v

        # L2 loss
        loss = 0.5 * (curr_q - target_q).pow(2).mean()
        return loss

loss を計算したら、ネットワークを更新しましょう！ログ記録などの実験管理に関連する処理は、アルゴリズムの責務ではないので、アルゴリズム側ではなく実験を行う側で行うことが望ましいでしょう。そのため、呼び出し側で loss を記録できるよう返します。

    def update(self, batch):
        # バッチサイズ分のデータ
        state, action, reward, done, next_state = batch

        # loss を計算する。
        loss = self.calculate_loss(state, action, reward, done, next_state)

        # ネットワークを更新する。
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        return {"loss": loss.item()}

update_target(self)

ターゲットネットワークの更新は、単にネットワークのパラメータを代入するだけです。

    def update_target(self):
        self.target_net.load_state_dict(self.q_net.state_dict())

これで、DQN クラスの実装が終わりました！このクラスでは、類似のアルゴリズムを実装する際に "特定のメソッドのみを書き換えるだけでアルゴリズムを実装・置き換えることができる" ように実装しました。ただし、"どの程度抽象化するべきか" は、ユースケースや実装したいアルゴリズムにもよるでしょう。より抽象度を高めて、たくさんのアルゴリズムを実装していきたい場合には、rllib が非常に参考になると思います。

メインプロセス

最後に、実際に学習を行うプロセスを実装しましょう！まずは、実験のハイパーパラメータを定義します。どのくらい環境で行動を行うかは NUM_STEPS で指定しています。ここでは、例として 100 万ステップ分行動させていますが、実際の DQN の論文では、Atari の環境で 2 億ステップ分行動させたりしています。

ENV_NAME = "MinAtar/Breakout-v1"
NUM_STEPS = 1000000
LEARNING_RATE = 0.00025
BATCH_SIZE = 32
BUFFER_SIZE = 100000
EPSILON = 0.01
GAMMA = 0.99
START_STEPS = 100000
UPDATE_INTERVAL = 1
TARGET_UPDATE_INTERVAL = 1000
LOG_DIR = os.path.join("logs", ENV_NAME, datetime.now().strftime("%Y-%m-%d-%H%M"))

# モデルを保存するディレクトリを作成する。
if not os.path.exists(os.path.join(LOG_DIR, "model")):
    os.makedirs(os.path.join(LOG_DIR, "model"))

次に、環境やリプレイバッファ、ネットワークなどのインスタンスを作成します。今回は、TensorBoard を使用してログを記録します。

# torch.tensor をのせるデバイス (GPU or CPU)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 環境
env = PyTorchEnv(gym.make(ENV_NAME))

# リプレイバッファ
buffer = ReplayBuffer(BUFFER_SIZE, env.observation_space, device)

# ネットワーク
q_net = QNetwork(env.action_space.n).to(device)
target_net = QNetwork(env.action_space.n).to(device)

# アルゴリズム
algo = DQN(
    q_net=q_net,
    target_net=target_net,
    gamma=GAMMA,
    start_steps=START_STEPS,
    epsilon=EPSILON,
    update_interval=UPDATE_INTERVAL,
    target_update_interval=TARGET_UPDATE_INTERVAL,
    lr=LEARNING_RATE,
)

# ログを記録するための Writer
writer = SummaryWriter(log_dir=os.path.join(LOG_DIR, "summary"))

実際に学習を行う部分は、以下のように実装できます。今後、類似のアルゴリズムを実装する場合には、algo のみを置き換えるだけで学習を実現できます。

# ログ用の統計
episode = 1
episode_reward = 0.0
episode_reward_stats = deque(maxlen=400)

# 環境を初期化して、初期状態を取得する。
state = env.reset()

for step in range(1, NUM_STEPS + 1):

    # 探索するかどうか
    if algo.is_random(step):
        # ランダムに探索する。
        action = np.random.randint(env.action_space.n)
    else:
        # 現時点で最適な行動を選択する。
        action = algo.q_net.select_action(
            torch.tensor(state, dtype=torch.float32, device=device)
        )

    # 環境を 1 時刻進める。
    next_state, reward, done, _ = env.step(action)
    # リプレイバッファにデータを保存する。
    buffer.append(state, action, reward, done, next_state)
    # 状態を更新する。
    state = next_state
    # ログ用に、エピソード全体の累積報酬を計算する。
    episode_reward += reward

    # エピソードが終了した場合
    if done:
        # 環境を初期化する。
        state = env.reset()
        # ログを記録する。
        episode_reward_stats.append(episode_reward)
        episode += 1
        episode_reward = 0.0

        # 定期的にログを書き出す。
        if episode % 400 == 0:
            episode_reward = np.mean(episode_reward_stats)
            writer.add_scalar("reward/episode_reward", episode_reward, step)
            print(f"Step {step} / Episode reward {episode_reward:.3f}")

    # ネットワークを更新する場合
    if algo.is_update(step):
        # バッチサイズ分のデータをサンプルする。
        batch = buffer.sample(BATCH_SIZE)
        # ネットワークを更新し、情報を受け取る。
        stats = algo.update(batch)

        # 定期的にログを書き出す。
        if step % 1000 == 0:
            writer.add_scalar("loss/q", stats["loss"], step)

        # 定期的にモデルを保存する。
        if step % 50000 == 0:
            torch.save(
                algo.q_net.state_dict(),
                os.path.join(LOG_DIR, "model", f"step{step}.pth")
            )

    # 定期的にターゲットネットワークを更新する。
    if algo.is_update_target(step):
        algo.update_target()

これでついに完成です！それでは、実際に学習させてみましょう。参考までに、僕が実験した際の学習時間を示しておきます。

• SageMaker Studio Lab
  • CPU ランタイム : 54min 58s
  • GPU ランタイム : 32min 33s
• Colab
  • GPU 利用なし : 1h 34min 49s
  • GPU 利用時 (K80) : 1h 4min 23s

学習結果

皆さん、学習結果を可視化してみましょう！今回は、loss とエピソードの累積報酬を TensorBoard に書き込んでいますので、これを可視化してみます。Jupyter Notebook を利用している場合には、以下のコマンドで TensorBoard を描画できます。

# TensorBoard を描画する。
%load_ext tensorboard
%tensorboard  --logdir {os.path.join(LOG_DIR, "summary")}

例えば、エピソード全体の累積報酬の推移は以下のように可視化されます。

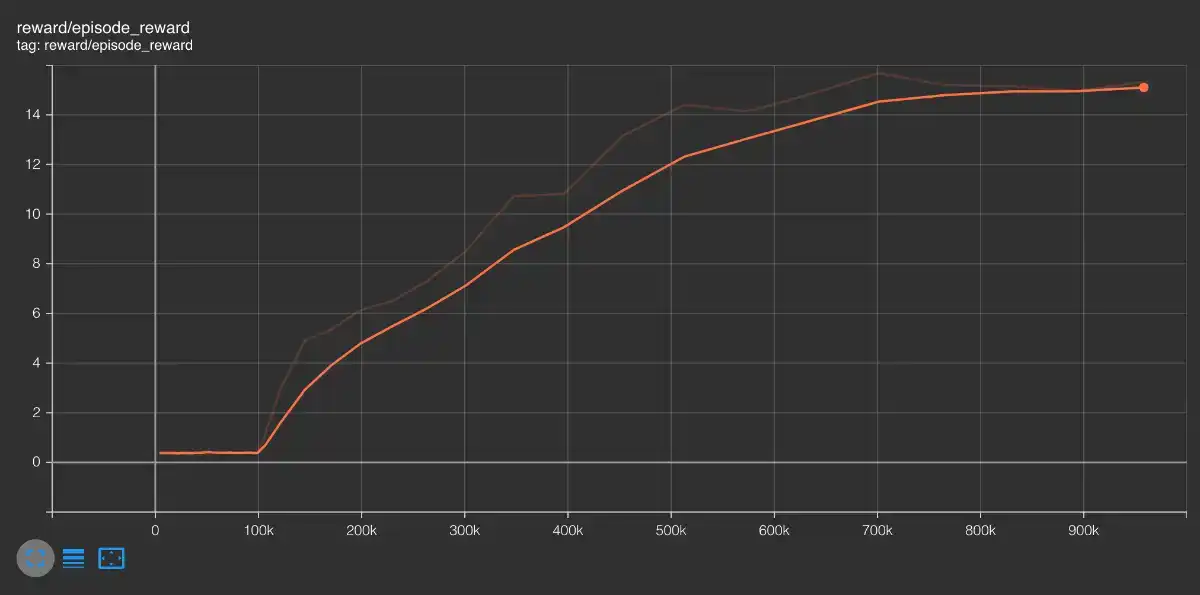
SageMaker Studio Lab をご利用の場合は、Notebook 上に TensorBoard が描画されません。その場合、SageMaker Studio Lab を開いているブラウザの URL の末尾の /lab 以下を /proxy/6006/ に変更した URL を開くことで、TensorBoard にアクセスできます。

• 変更前 : https://.../studiolab/default/jupyter/lab/...
• 変更後 : https://.../studiolab/default/jupyter/proxy/6006/

また、学習後のエージェントで、実際にゲームをプレイさせてみましょう。デスクトップ環境であれば env.render メソッドでゲーム画面を可視化できます。ここでは、リモートの Jupyter Notebook 環境でも簡単に可視化できるよう、mp4 形式で保存してあげます。

gym.wrappers.RecordVideo を利用すると、簡単に動画を mp4 で保存できます。ただし、RecordVideo は gym=>0.20.0 でのみ利用可能です。また、MinAtar は mp4 作成に対応していないので、mp4 に対応するように修正した環境を利用してください。

# 検証用に動かすエピソード数
NUM_EPISODES = 5

# テスト用の環境を、mp4 保存するようにラップする。
env = gym.wrappers.RecordVideo(
    PyTorchEnv(gym.make(ENV_NAME)),
    os.path.join(LOG_DIR, "video"),
    episode_trigger=lambda x: True
)


state = env.reset()
episode = 0
episode_reward = 0.0

while episode < NUM_EPISODES:
    action = q_net.select_action(torch.tensor(state, dtype=torch.float32, device=device))
    next_state, reward, done, _ = env.step(action)
    state = next_state
    episode_reward += reward

    if done:
        print(f"Episode reward {episode_reward:.3f}")
        state = env.reset()
        episode_reward = 0.0
        episode += 1

env.close()

上のコードを実行すると、os.path.join(LOG_DIR, "video") 配下に各エピソードの動画が保存されます。以下の関数で描画してあげましょう！おそらく 100 万ステップの学習では "うまくいったりいかなかったり" だと思うので、いくつか保存されている動画を、それぞれ可視化してみてください。

from base64 import b64encode
from IPython.display import HTML

def play_mp4(path):
    # path にある mp4 を再生する。
    mp4 = open(path, 'rb').read()
    url = "data:video/mp4;base64," + b64encode(mp4).decode()
    return HTML("""<video width=400 controls><source src="%s" type="video/mp4"></video>""" % url)

# 下のセルでエラーが出る場合には、`imageio-ffmpeg` をインストールしてください。
# !pip install imageio-ffmpeg==0.4.7

# 動画を再生する例 (ファイル名は、適宜変更してください。)
play_mp4(os.path.join(LOG_DIR, "video", "rl-video-episode-0.mp4"))

この記事の最初に載せている動画は、実際に僕が学習させたエージェントの動画 (のうち、いい感じのもの) です。皆さんのエージェントはうまくプレイできていますか？

初めての強化学習実装、お疲れ様でした！

まとめ

この記事では、実際に DQN を実装してみることで、強化学習の全体像や実装の大まかな流れを学びました。特に、"今後ご自身で他のアルゴリズムを実装する" ための第一歩として、僕の経験に基づく考え方や Tips をお伝えしました。皆さんが、少しでも強化学習に興味を持っていただけていたら嬉しいです。

ぜひ、これを機に強化学習の世界にも足を踏み入れてみましょう。例えば、強化学習が使えそうな Kaggle コンペに参加してみたり、日本の強化学習コミュニティ (強化学習若手の会や強化学習苦手の会など) に参加してみるのも良いでしょう。

今後もこのような記事をどんどん書いていくつもりなので、もし改善のためのフィードバックがあれば、ぜひお待ちしています！

では、また。